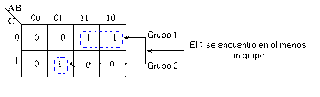MAPA DE KARNAUGH
Introducción
El método de Karnaugh convierte una expresión a otra más simplificada. En nuestro caso, convierte una suma de productos en otra mínima denominada Minimal Sum Product (MSP o suma de productos minimal) . Tiene como características:
o Un mínimo número de términos en la expresión.
o Un mínimo número de variables en cada término de dicha expresión.
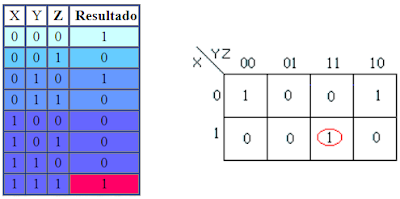
Inicialmente poseemos una expresión booleana constituida por una suma de productos de variables, que pueden tomar únicamente los valores de cero o uno. El resultado de esta expresión es un valor booleano para cada uno de los valores que tomen dichas variables. Dichos valores se van almacenando en una tabla de verdad como la que ilustramos en el siguiente ejemplo:
F(x, y, z) = x y z + x’z’
Podemos hacer una representación gráfica de dicha tabla de verdad, mediante la matriz que se encuentra al lado, denominada mapa de Karnaugh. Así el resultado en rojo obtenido en la tabla de verdad se corresponde con la posición indicada en rojo en la matriz. Cada valor en esta matriz recibe el nombre de implicante siendo los valores uno minterm.
Reglas de simplificación
1. Las agrupaciones son exclusivamente de unos. Esto implica que ningún grupo puede contener ningún cero.
2. Las agrupaciones únicamente pueden hacerse en horizontal y vertical. Esto implica que las diagonales están prohibidas.
3. Los grupos han de contener 2n elementos. Es decir que cada grupo tendrá 1,2,4,8... número de unos.
4. Cada grupo ha de ser tan grande como sea posible. Tal y como lo ilustramos en el ejemplo.
5. Todos los unos tienen que pertenecer como mínimo a un grupo. Aunque pueden pertenecer a más de uno.
6. Pueden existir solapamiento de grupos.
7. La formación de grupos también se puede producir con las celdas extremas de la tabla. De tal forma que la parte inferior se podría agrupar con la superior y la izquierda con la derecha tal y como se explica en el ejemplo.
8. Tiene que resultar el menor número de grupos posibles siempre y cuando no contradiga ninguna de las reglas anteriores. Esto es el número de grupos ha de ser minimal.
Metodología
Vamos a indicar cada uno de los pasos para obtener la expresión MSP (mínima suma de productos). Para ello vamos a ilustrarlo con el ejemplo:
F(x, y, z) = x’ y’ z’ + x’ y’ z + x’ y z’+ x y’ z’+ x y z’
Los pasos a seguir para conseguir reducir esta expresión son:
1. Convertir la expresión a una suma de productos si es necesario. Esto se puede realizar de varias maneras:
- Algebraicamente.
- Construyendo una tabla de verdad, trasladando los valores al mapa de Karnaugh. Esta es la forma que vamos a utilizar.
2. Cubrir todos los unos del mapa mediante rectángulos de 2N elementos, donde N = 0 ... número de variables. Ninguno de esos rectángulos debe contener ningún cero (tal y como indicábamos en el apartado anterior).
- Para minimizar el número de términos resultantes se hará el mínimo número posible de rectángulos que cubran todos los unos.
- Para minimizar el número de variables se hará cada rectángulo tan grande como sea posible.
Véase que en este caso se ha unido la columna izquierda con la derecha para formar un único rectángulo.
3. Encontrar la MSP (suma de productos minimal). Ojo porque podemos encontrarnos con que puede haber más de una MSP.
- Cada rectángulo pertenece a un término producto.
- Cada término se define encontrando las variables que hay en común en tal rectángulo.
En nuestro ejemplo tenemos F(X, Y, Z) = Z’ + X’Y’ nótese que las variables resultado son las que tienen un valor común en cada rectángulo.
Rectángulos y productos.
Cada rectángulo representa un término. El tamaño del rectángulo y el del término resultante son inversamente, es decir que, cuanto más largo sea el rectángulo menor será el tamaño del término final.
En general, si tenemos una función con n variables :
- Un rectángulo que ocupa una celda equivale a un término con n variables.
- Un rectángulo que ocupa dos celdas equivale a un término con n-1 variables.
- Un rectángulo que ocupa 2n celdas equivale al término de valor 1.
Por lo tanto, para encontrar el MSP se debe:
- Minimizar el número de rectángulos que se hacen en el mapa de Karnaugh, para minimizar el número de términos resultantes.
- Maximizar el tamaño de cada rectángulo, para minimizar el número de variables de cada término resultante.
Agrupación de rectángulos.
Cuando tenemos distintas posibilidades de agrupar rectángulos hay que seguir ciertos criterios:
- Localiza todos los rectángulos más grandes posibles, agrupando todos los unos. Estos se llamarán implicantes primos.
- Si alguno de los rectángulos anteriores contiene algún uno que no aparece en ningún otro rectángulo entonces es un implicante primo esencial. Éstos han de aparecer en el resultado final de manera obligatoria.
El resto de implicantes primos se podrán combinar para obtener distintas soluciones.
Véase este ejemplo que ilustra lo que les planteamos. Aquí los implicantes primos son cada uno de los diferentes rectángulos obtenidos. Los primos implicantes esenciales son el rectángulo rojo y el verde, por contener unos que no son cubiertos por otros rectángulos. Así todas las posibles soluciones han de contener estos dos implicantes.
Solución: F( X, Y, Z, T ) = X’Y’ + XYT’ + XZT